LeNet：第一个卷积神经网络

　　「识别手写数字」是一个经典的机器学习任务，有著名的 MNIST 数据集。我们曾经利用多层感知机实现了 90+% 的准确率，本文将介绍卷积神经网络 LeNet，主要参考这篇英文博客的讲解。

　　LeNet 是几种神经网络的统称，它们是 Yann LeCun 等人在 1990 年代开发的。一般认为，它们是最早的卷积神经网络（Convolutional Neural Networks, CNNs）。模型接收灰度图像，并输出其中包含的手写数字。LeNet 包含了以下三个模型：

LeNet-1：5 层模型，一个简单的 CNN。
LeNet-4：6 层模型，是 LeNet-1 的改进版本。
LeNet-5：7 层模型，最著名的版本。

　　CNN 的设计是为了模拟人眼的感知方式。传统的 CNN 一般包含以下三种层：

卷积层（convolution layers）
降采样层（subsampling layers），或称池化层（pooling layers）
全连接层（fully connected layers）

　　它们有各自的用途，通过排列这些层，我们能实现各种 CNN。接下来，我们分别介绍这三种部件。

卷积层

　　卷积层利用卷积核（kernel，或称 filter）对图像进行卷积运算。每个 kernel 都是可训练的，有些 kernel 还有 bias 参数。执行卷积运算时，把 kernel 在原图上移动，步长为指定的参数 stride，有时还会做 padding。对于原图内容，将其与 kernel 先进行元素乘法，把结果求和，再加上 bias，就得到输出。

　　把原图跑完一遍之后，我们在各个位置的卷积结果，生成了特征图（feature map）。显然，kernel 越大，步长越长，padding 越小，则特征图越小。具体而言，满足：$$\text{output size} =\frac{\text{input size} - \text{kernel size} + 2\times \text{padding}}{\text{stride}} + 1$$

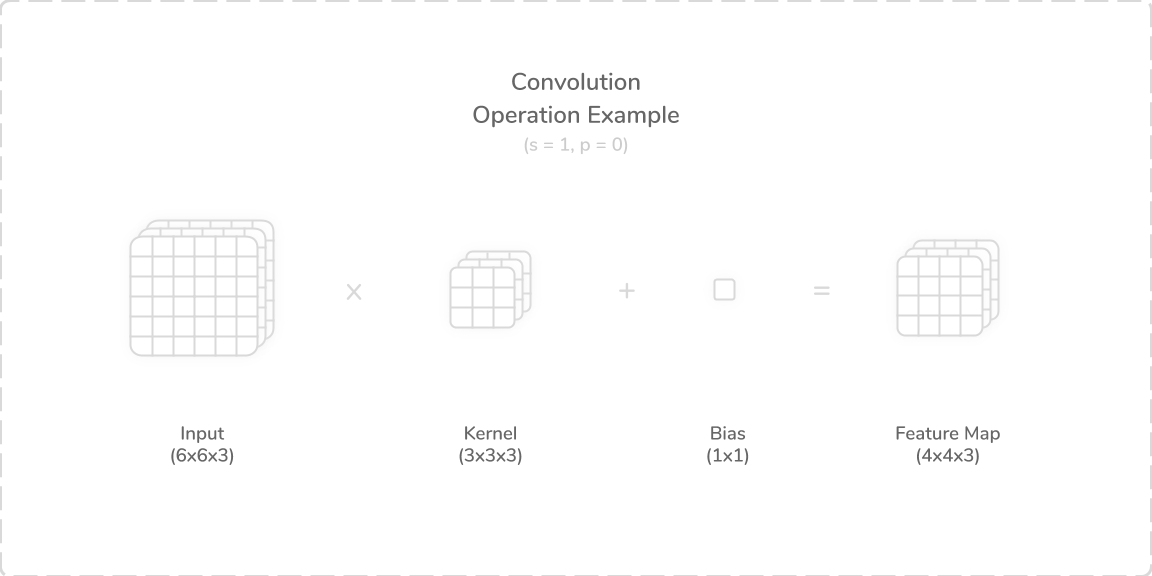
卷积运算。原图和 kernel 均有 3 个通道。图片来源：Azel Daniel，下同。

　　上图展示了一个典型的二维卷积。原图是 3 通道的，不填充，步长为 0。最终将生成 4×4 的 3 通道特征图。

池化层

　　池化层一般是不用训练的。它的目的是对特征进行降取样，显著减少特征的个数来方便学习。一般有两种池化方式：均值池化（average pooling）和最大池化（max pooling）。前者计算出一个区域的均值，后者从区域中取最大值。

　　上图展示了一个不填充、步长为 2 的池化。6×6×3 的原图在池化之后，变成了 3×3×3 的大小。

全连接层

　　全连接层一般用于 CNN 的最后几层，负责提取卷积和池化之后的特征。这里不过多介绍。接下来，我们开始讨论几种 LeNet。

LeNet-1

　　LeNet-1 仅有五个层，结构如下：

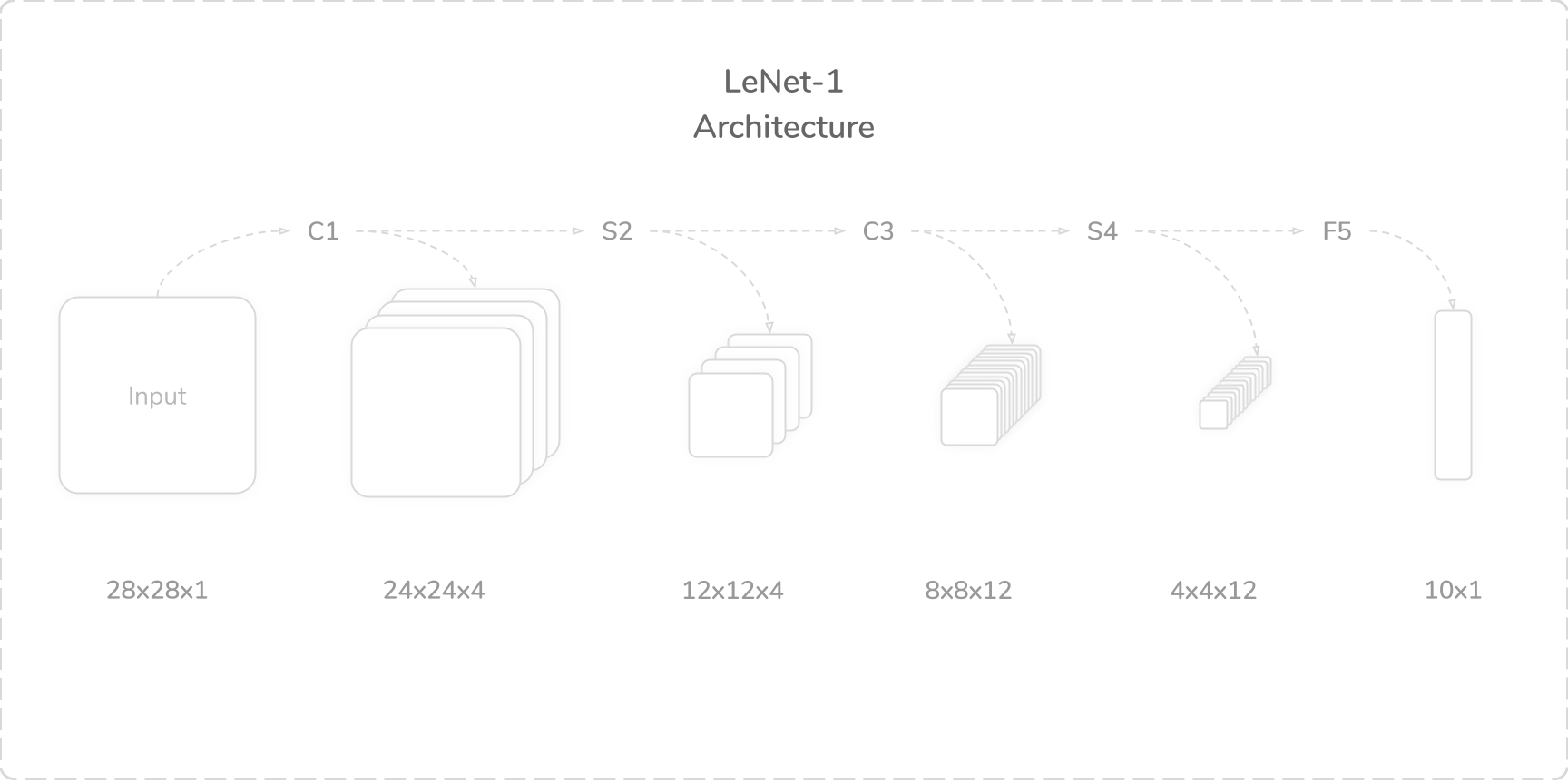
　　原先的 28×28 的灰度图像，先经过一个卷积层，生成 4 通道的 feature map；再进行池化降维，然后通过卷积层，得到 12 通道的 feature map。再次池化之后，用全连接层提取特征。具体参数如下：

C1：卷积层，num_kernels=4, kernel_size=5×5, padding=0, stride=1
S2：均值池化层，kernel_size=2×2, padding=0, stride=2
C3：卷积层，num_kernels=12, kernel_size=5×5, padding=0, stride=1
S4：均值池化层，kernel_size=2×2, padding=0, stride=2
F5：全连接层，out_features=10

　　我们需要解释一下 C3 如何用 12 个 kernel，从 4 通道的图中提取出 12 个通道的特征。C3 的每个输出层，是与指定的一些 S2 层相连的，对应的 kernel 长宽是 5×5×n，其中 n 是它所连接的 S2 层数。连接分组方式是超参数（当然我们经常懒得去搞这件事，往往令每个输出层与所有输入层相连，下面的代码也是这样处理的）。

import torch
import torchvision
import torch.nn as nn
import torchvision.transforms as transforms
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt

trans_to_tensor = transforms.Compose([
    transforms.ToTensor()
])

data_train = torchvision.datasets.MNIST(
    './data', 
    train=True, 
    transform=trans_to_tensor, 
    download=True)

data_test = torchvision.datasets.MNIST(
    './data', 
    train=False, 
    transform=trans_to_tensor, 
    download=True)

data_train, data_test

'''
(Dataset MNIST
     Number of datapoints: 60000
     Root location: ./data
     Split: Train
     StandardTransform
 Transform: Compose(
                ToTensor()
            ),
 Dataset MNIST
     Number of datapoints: 10000
     Root location: ./data
     Split: Test
     StandardTransform
 Transform: Compose(
                ToTensor()
            ))
'''

▲ 加载数据

　　我们随便展示一个数据：

train_loader = torch.utils.data.DataLoader(data_train, batch_size=100, shuffle=True)

x, y = next(iter(train_loader))

plt.imshow(x[0].squeeze(0), cmap='gray'), y[0]

　　训练网络：

def test(net):
    net.eval()
    
    test_loader = torch.utils.data.DataLoader(data_train, batch_size=10000, shuffle=False)
    test_data = next(iter(test_loader))
    
    with torch.no_grad():
        x, y = test_data[0], test_data[1]
    
        outputs = net(x)

        pred = torch.max(outputs, 1)[1]
        print(f'test acc: {sum(pred == y) / outputs.shape[0]}')
    
    net.train()
    
def fit(net, epoch=1):
    net.train()
    run_loss = 0
    
    for num_epoch in range(epoch):
        print(f'epoch {num_epoch}')
        
        for i, data in enumerate(train_loader):
            x, y = data[0], data[1]

            outputs = net(x)
            loss = criterion(outputs, y)

            optimizer.zero_grad()
            loss.backward()
            optimizer.step()

            run_loss += loss.item()

            if i % 100 == 99:
                print(f'[{(i+1) * 100} / 60000] loss={run_loss / 100}')
                run_loss = 0
                
                test(net)

　　上面是训练 MNIST 的通用框架。接下来我们实现 LeNet-1：

class LeNet1(nn.Module):
    
    def __init__(self):
        super().__init__()
        
        self.conv1 = nn.Conv2d(1, 4, [5, 5])
        self.pool1 = nn.AvgPool2d([2, 2])
        self.conv2 = nn.Conv2d(4, 12, [5, 5])
        self.pool2 = nn.AvgPool2d([2, 2])
        self.fc1 = nn.Linear(12 * 4 * 4, 10)
    
    def forward(self, x):
        x = torch.tanh(self.conv1(x))
        x = self.pool1(x)
        x = torch.tanh(self.conv2(x))
        x = self.pool2(x)
        x = x.view(-1, 12 * 4 * 4)
        x = self.fc1(x)
        
        return x

net_1 = LeNet1()

criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net_1.parameters())

fit(net_1, epoch=5)

'''
epoch 0
[10000 / 60000] loss=1.3996468645334244
test acc: 0.8370000123977661
[20000 / 60000] loss=0.525577874481678
test acc: 0.8773999810218811
[30000 / 60000] loss=0.40644764140248296
test acc: 0.8932999968528748
[40000 / 60000] loss=0.367893455773592
test acc: 0.9024999737739563
[50000 / 60000] loss=0.3431669014692307
test acc: 0.9133999943733215
[60000 / 60000] loss=0.30854775562882425
test acc: 0.916100025177002

....

epoch 4
[10000 / 60000] loss=0.1185341552272439
test acc: 0.9692000150680542
[20000 / 60000] loss=0.10541347645223141
test acc: 0.968999981880188
[30000 / 60000] loss=0.107633958440274
test acc: 0.9714000225067139
[40000 / 60000] loss=0.10533566184341908
test acc: 0.9721999764442444
[50000 / 60000] loss=0.10117398623377084
test acc: 0.9725000262260437
[60000 / 60000] loss=0.09958926556631922
test acc: 0.9736999869346619
'''

　　可见 LeNet-1 的准确度还是很高的，训练 20 个 epoch 之后可以达到 98.90% 的准确率。另外，我没有调超参数，调一调之后还可以涨更多的点，Github 上有网友的代码的 batchsize 是 64，拿了99.30% 准确率。从 Adam 换成 SGD 也许可以再涨一些点。

　　接下来要问：卷积起到了什么作用？我们知道，卷积可以完成很多操作，例如高斯模糊、边缘提取等，这是因为卷积是对原图中一块相邻区域的运算。传统的多层感知机，对像素位置之间的关联是很弱的，而卷积层输出的 feature map 中，每个值都是由原图中的一个块产生，故考虑了相邻像素之间的关系。

　　下面展示两张图片经过 conv1 层之后的结果：

　　可以发现，第一个 kernel 可以很好地提取「左上－右下」的线条；第二、三个 kernel 可以提取横向的线条；第四个 kernel 可以提取「左下－右上」的线条。这不是我们钦定的，而是它们自己学习出来的。我们从中可以体会到 CNN 提取图片「部件」的独到之处。

LeNet-4

　　LeNet-4 是 LeNet-1 的改进版本，有 6 个层。它们主要的不同之处在于，LeNet-4 采用了两个全连接层来提取特征。另外，LeNet-4 的输入是 32×32 的灰度图。

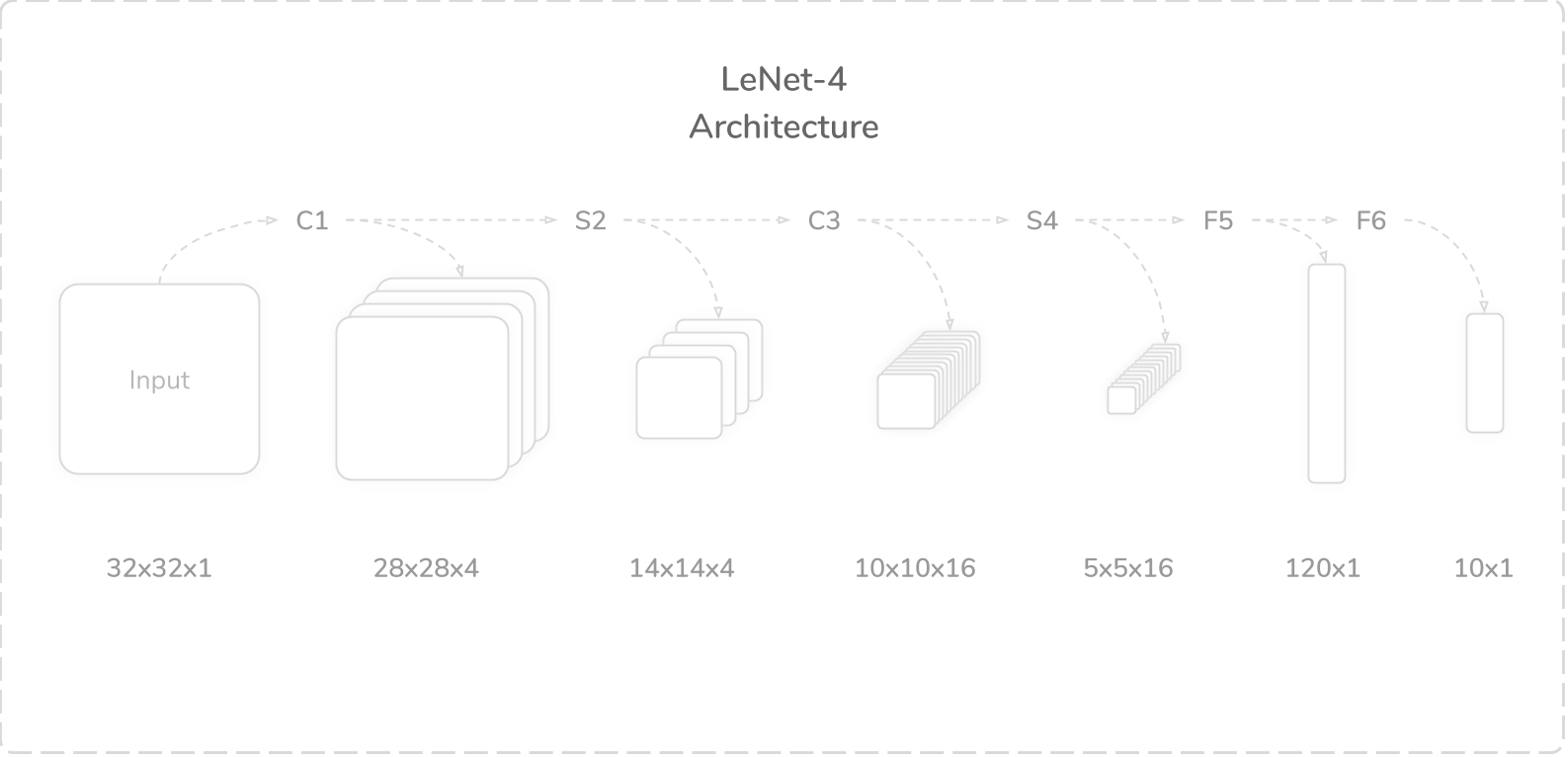
　　每个层的参数如下：

C1：卷积层，num_kernels=4, kernel_size=5×5, padding=0, stride=1
S2：均值池化层，kernel_size=2×2, padding=0, stride=2
C3：卷积层，num_kernels=16, kernel_size=5×5, padding=0, stride=1
S4：均值池化层，kernel_size=2×2, padding=0, stride=2
F5：全连接层，out_features=120
F6：全连接层，out_features=10

　　Yann LeCun 在 USPS 数据集上，测得 LeNet-1 的误判率是 1.7%，有 3246 个参数；LeNet-4 在 MNIST 上的误判率是 1.1%，但有 51050 个参数。像这种架构的 CNN，全连接层占了绝大部分的参数。

LeNet-5

　　LeNet-5 是 LeNet-4 的改进版，即现在我们熟知的那个 LeNet。它的层数达到了 7 层，获取 32×32 的输入，有 60850 个参数。

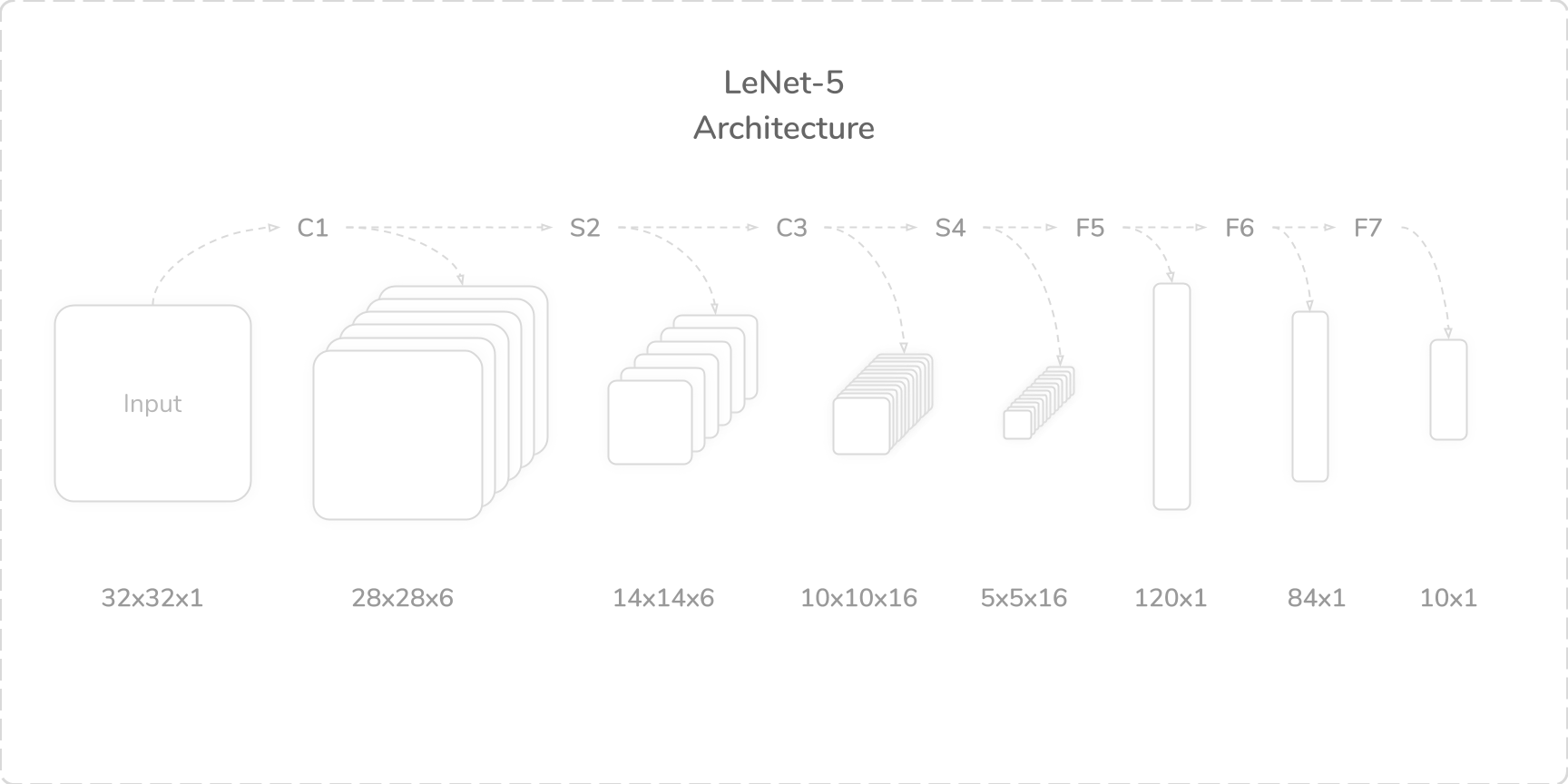
　　在 MNIST 数据集上，Yann LeCun 的 LeNet-5 具有 0.95% 的低误判率。其各层参数如下：

C1：卷积层，num_kernels=6, kernel_size=5×5, padding=0, stride=1
S2：均值池化层，kernel_size=2×2, padding=0, stride=2
C3：卷积层，num_kernels=16, kernel_size=5×5, padding=0, stride=1
S4：均值池化层，kernel_size=2×2, padding=0, stride=2
F5：全连接层，out_features=140
F6：全连接层，out_features=84
F7：全连接层，out_features=10

　　S2 层有个需要注意的地方：它的每一个输出通道，是由对应的输入通道的池化结果，乘以 weight 再加上 bias。它们都是可训练的，于是 S2 层有了 12 个可训练参数（共 6 个通道，每个通道训练自己的 weight 和 bias）。S4 层与之类似，有 32 个可训练参数。

　　C3 的每个输出通道，只与 S2 指定的若干个通道相连。具体的分组方法如下：

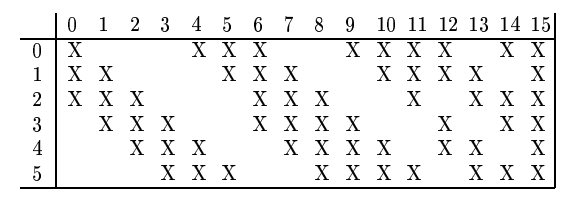
　　我们在代码里面继续偷懒，让 C3 的每个输出通道与 S2 所有通道相连。另外，由于 LeNet-5 输入为 32×32，而我们手上的 MNIST 是 28×28 的，于是做 2 像素的 padding，来形成 32×32 的图。

class LeNet5(nn.Module):
    
    def __init__(self):
        super().__init__()
        
        self.conv1 = nn.Conv2d(1, 6, 5, padding=2)
        self.pool1 = nn.AvgPool2d(2)
        self.conv2 = nn.Conv2d(6, 16, 5)
        self.pool2 = nn.AvgPool2d(2)
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        x = torch.tanh(self.conv1(x))
        x = self.pool1(x)
        x = torch.tanh(self.conv2(x))
        x = self.pool2(x)
        
        x = x.view(-1, 16 * 5 * 5)
        x = self.fc1(x)
        x = self.fc2(x)
        x = self.fc3(x)
        
        return x

net_5 = LeNet5()

criterion = nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net_5.parameters())

fit(net_5, epoch=20)

'''
epoch 0
[10000 / 60000] loss=0.8946414443850518
test acc: 0.8745999932289124
[20000 / 60000] loss=0.3811839409172535
test acc: 0.9031000137329102
[30000 / 60000] loss=0.34581568479537966
test acc: 0.9114999771118164
[40000 / 60000] loss=0.299122948423028
test acc: 0.9218000173568726
[50000 / 60000] loss=0.25059412196278574
test acc: 0.927299976348877
[60000 / 60000] loss=0.22540301881730557
test acc: 0.9373000264167786

...

epoch 19
[10000 / 60000] loss=0.024130959606263786
test acc: 0.9918000102043152
[20000 / 60000] loss=0.02669174194626976
test acc: 0.9901000261306763
[30000 / 60000] loss=0.02360637279227376
test acc: 0.9883000254631042
[40000 / 60000] loss=0.023022194614750333
test acc: 0.9933000206947327
[50000 / 60000] loss=0.035112172679509966
test acc: 0.9896000027656555
[60000 / 60000] loss=0.03023288542899536
test acc: 0.9898999929428101
'''

　　注意到 LeNet-5 的泛化能力确实比 LeNet-1 好了一些，这边迭代 20 次之后，可以涨到 99.33% 的准确率。

　　来看 conv1 处理之后的结果：

　　这里我们可以看出，kernel 3、5 可以提取上边缘，kernel 4 可以提取下边缘。kernel 1 可以提取竖线，kernel 2 可以提取横线。

　　Yann LeCun 训练这些 LeNet 的时候，对数据进行了预处理，使之均值为 0，方差大概为 1。另外，当时采用的是 MSE loss，本文采用了交叉熵。LeNet 是一个划时代的模型，但它也有一些不足之处：

网络很小，限制了应用场景。
LeNet 采用了均值池化，但我们现在倾向于采用最大池化，这样可以加速收敛。
LeNet 采用的激活函数是 tanh，但我们现在倾向于使用 ReLU。实践上，ReLU 往往能够有更好的正确率。

　　总结一句，LeNet 给我们提供的思路是：用卷积提取与位置相关的信息；用池化来减少特征数量；用全连接来提取特征、进行预测。

LeNet：第一个卷积神经网络

Ruan Xingzhi

Ruan Xingzhi

卷积层

池化层

全连接层

LeNet-1

LeNet-4

LeNet-5

《情感计算》命题报告

LLM Riddles 民间题解

训练一个 GAN

训练一个 GAN

欺骗神经网络