今天我们来研究 lattice. 首先给一个定义:
格(lattice) 设 $\newcommand\v{\boldsymbol{v}} \newcommand\vn{\v_1 \newcommand\do{,\dots,} \do \v_n} \vn \in \newcommand\R{\mathbb{R}} \R ^ m$ 是线性无关向量组。我们称 $\vn$ 生成(generate) 了 lattice $L$:$$L = \{a_1 \v_1 + a_2 \v_2 +\cdots+ a_n \v_n : a_1, a_2\do a_n \in \newcommand\Z{\mathbb{Z}} \Z\}$$即 $L$ 中的元素是 $\vn$ 的整系数线性组合。
我们定义 $L$ 的一个基(basis)是任何一个能生成 $L$ 的向量组。显然 lattice 的两个基会拥有相同的向量个数;基所包含的的向量个数称为 $L$ 的纬度(dimension).
我们在线性空间中研究过基变换,现在我们也来看一下 lattice 中两个基的关系。假设 $\vn$ 是 lattice $L$ 的一个基,而 $\newcommand\b{\boldsymbol} \newcommand\w{\b w} \newcommand\wn{\w_1\do\w_n} \wn$ 是 $L$ 中的一个向量组。接下来将 $\w_j$ 表示成 $\v_i$ 的线性组合:$$\begin{aligned} \w_1 &= a_{11}\v_1 + a_{12}\v_2 + \cdots + a_{1n} \v_n \\ \w_2 &= a_{21}\v_1 + a_{22}\v_2 + \cdots + a_{2n} \v_n \\ \vdots ~~ & \qquad\qquad\qquad\vdots \\ \w_n &= a_{n1}\v_1 + a_{n2}\v_2 + \cdots + a_{nn} \v_n \end{aligned}$$由于 $\w_j$ 是 lattice 中的向量,这里的系数 $a_{ij}$ 全部是整数。
接下来,我们考虑能不能使用 $\w_j$ 来组合出 $\v_i$. 来考虑下面的矩阵:$$U = \begin{pmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{pmatrix}$$显然 $U\cdot V = W$,于是利用 $\w_i$ 表达 $\v_i$,系数是 $U^{-1}W$. 但 lattice 中,线性组合的系数必须全都是整数,于是 $U^{-1} $ 里面的元素也必须全部是整数。注意到 $$1 = \det (I) = \det (U U ^{-1}) = \det(U) \det(U ^{-1})$$由行列式的(代数上的)定义式可以看出,如果一个矩阵元素全部是整数,那么行列式也必然是整数。从而 $\det(U), \det(U ^{-1})$ 都是整数,而它们的乘积为 1,这导致如下性质:
lattice $L$ 的任意两个基,其基变换矩阵中的元素均为整数,且行列式为 $\pm 1$.
我们比较喜欢研究向量全部都是整数坐标的那些 lattice,因为这会很大程度地方便计算。例如,$$\Z ^n = \{ (x_1, x_2\do x_n) : x_1\do x_n \in \Z\}$$ 就是包含了所有整数坐标向量的 lattice.
整格(integral lattice):一个 integral(or integer) lattice,是指所包含的向量都拥有整数坐标的 lattice. 或者说,一个 integral lattice,是 $\Z ^m$ 加法群的一个子群。
接下来我们举一个例子。考虑以下向量生成的 integral lattice $L$:$$\v_1 = (2, 1, 3), \quad\v_2 = (1, 2, 0),\quad \v_3 = (2, -3, -5)$$把它们作为行向量,写成矩阵:$$A=\begin{pmatrix} 2 & 1 & 3 \\ 1 & 2 & 0 \\ 2 & -3 & -5 \end{pmatrix}$$接下来考虑 $L$ 中的另一个向量组 $$\w_1 = \v_1 + \v_3,\quad \w_2 = \v_1 - \v_2 + 2\v_3,\quad \w_3 = \v_1 + 2\v_2$$于是有变换矩阵$$U=\begin{pmatrix} 1&0&1\\1&-1&2\\1&2&0 \end{pmatrix}$$从而可以计算出 $\w_1, \w_2, \w_3$:$$B = UA = \begin{pmatrix}4&-2&-2 \\ 5&-7&-7 \\ 4&5&3\end{pmatrix}$$我们注意到 $U$ 的行列式是 $-1$,从而 $\w_1, \w_2, \w_3$ 也是 $L$ 的一个基。现在利用 $\w_j$ 来组合出 $\v_i$,系数是 $U$ 的逆矩阵:$$U ^{-1} = \begin{pmatrix}4 & -2 & -1 \\ -2 &1&1 \\ -3&2&1\end{pmatrix}$$验证一下,果然有 $\v_1 = 4\w_1 - 2\w_2 - \w_3$. 其余类推。
v1 = [2, 1, 3]
v2 = [1, 2, 0]
v3 = [2, -3, -5]
A = matrix([v1, v2, v3])
print(A)
# [ 2 1 3]
# [ 1 2 0]
# [ 2 -3 -5]
U = matrix([[1, 0, 1], [1, -1, 2], [1, 2, 0]])
print(U)
# [ 1 0 1]
# [ 1 -1 2]
# [ 1 2 0]
print(U.det())
# -1
B = U*A
print(B)
# [ 4 -2 -2]
# [ 5 -7 -7]
# [ 4 5 3]
inv_U = U.inverse()
print(inv_U)
# [ 4 -2 -1]
# [-2 1 1]
# [-3 2 1]
assert inv_U * B == A总结一句:
- 若 $L\subset \R ^m$ 是一个 $n$ 维的 lattice,那么它的一个基可以被写成 $n\times m$ 矩阵 $A$.
- $L$ 的另一个基,可以通过 $A$ 左乘一个 $n\times n$ 的基变换矩阵来得到,其中 $U$ 必须是整系数矩阵,且行列式为 $\pm 1$. 满足这种条件的 $U$,称为 $\Z$ 上的一般线性群(general linear group),记为 $\text{GL} _n (\Z)$. 它是满足“逆矩阵也为整系数矩阵”的整系数矩阵的群。
接下来,我们在几何意义上定义 lattice.
加法子群(additive subgroup) 我们考虑 $\R ^m$ 的一个子集 $L$,它是加法子群当且仅当其在加法、减法运算上封闭。
离散加法子群(discrete additive subgroup) 称一个加法子群 $L$ 为离散加法子群,当且仅当存在一个正的常数 $\epsilon > 0$,使得$$\forall v\in L,\quad L \cap \{\w \in \R ^m : \|\v - \w\| < \epsilon\} = \{\v\}$$
上面这个式子的几何意义是:对于 $L$ 中的每一个点 $\v$,其附近 $\epsilon$ 的(欧几里得)距离范围内,不存在 $L$ 的其他点。也就是说 $L$ 是离散的,每两个点之间的距离都不小于某个(足够小的)$\epsilon$.
接下来我们有定理:
格(lattice) 一个 $\R ^m$ 的子集是 lattice,当且仅当它是离散加法子群。
证明我们略掉。总之,一个 lattice 与线性空间是非常相似的,除了 lattice 必须由 basis 的整系数线性组合来生成,而线性空间可以用任意实数作为线性组合系数。lattice 可以视为 $\R ^m$ 上的离散点集,如下图所示。
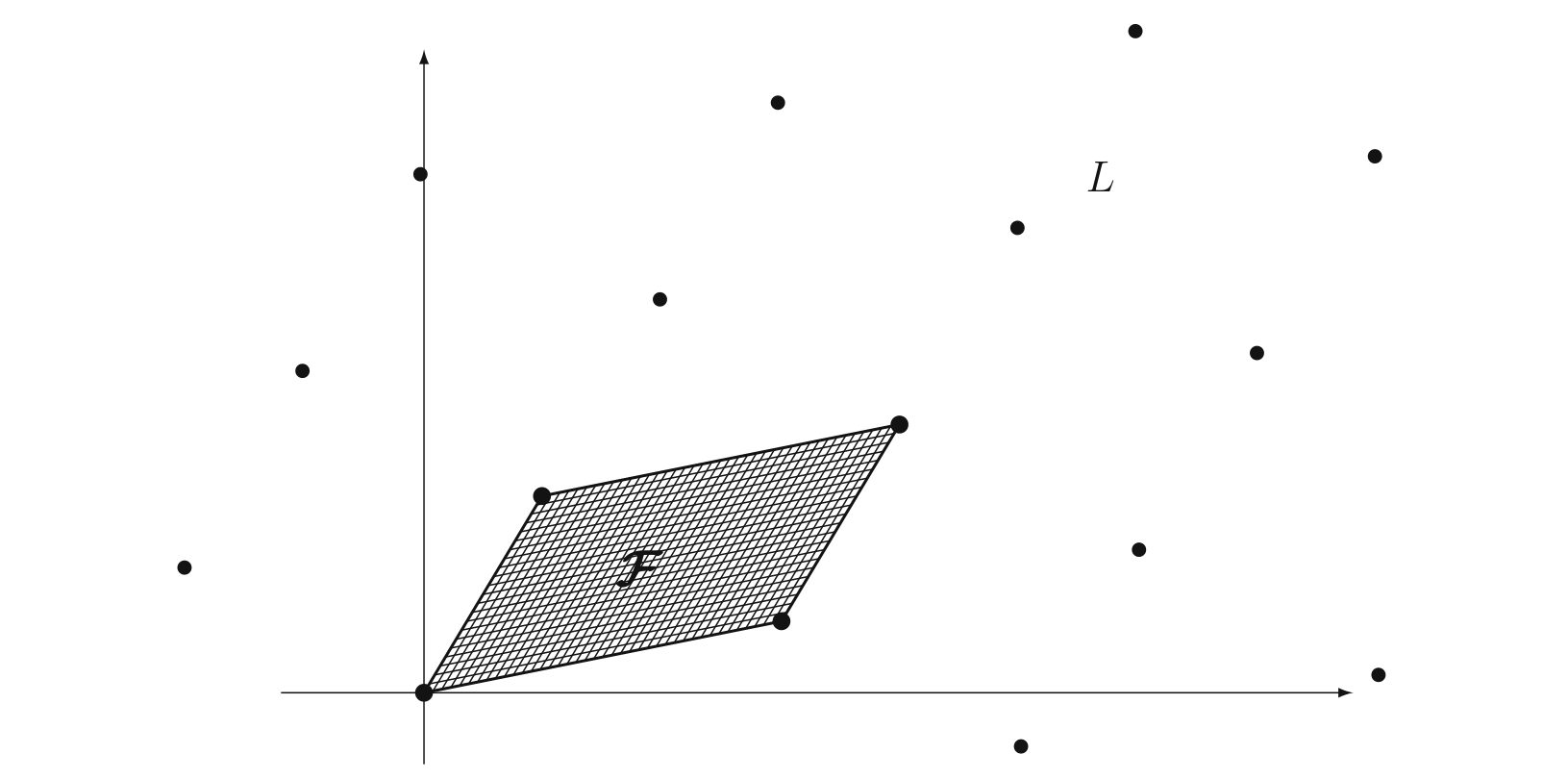
接下来,我们给出基本域的概念。
基本域(fundamental domain, fundamental parallelepiped)
设 $L$ 是一个 $n$ 维 lattice,$\vn$ 是一个基。则 $L$ 对应这一组基的基本域是 $$\newcommand\F{\mathcal{F}} \F(\vn) = \{t_1\v_1 + t_2\v_2 +\cdots+ t_n\v_n : 0\leq t_i \leq 1\}$$
几何上,基本域就是这组基围出的区域,如上图中的阴影部分。接下来我们讨论基本域的一条性质:
设 $L\subset \R ^n$ 是一个 $n$ 维 lattice,$\F$ 是 $L$ 的一个基本域。那么对于所有 $\w \in \R ^n$,它都可以写成如下形式:$$\w = \newcommand\t{\b t} \t+\v \quad\text{for a unique }~ t\in\F ~ \text{and a unique} ~ \v \in L$$需要注意到这里的 $\t, \v$ 都是唯一的。证明并不复杂。
另外,我们不难注意到,translated fundamental domains(不知道怎么翻译) $$\F + \v = \{\t + \v:\t \in \F\}$$在 $\v$ 取遍 $L$ 中的每一个点时,恰好覆盖了整个 $\R ^n$,如下图所示。
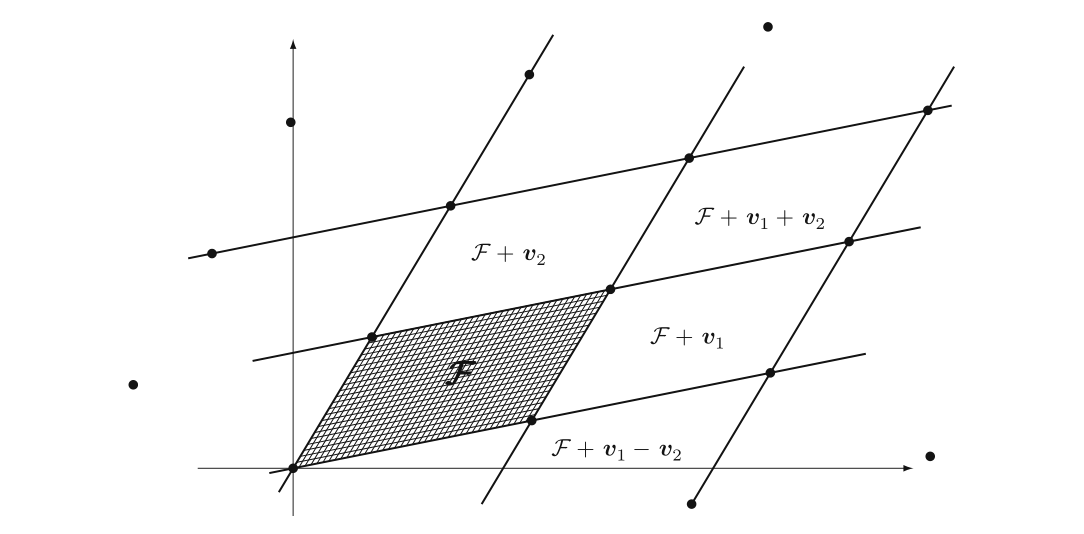
一个 lattice 会有不同的基,于是有不同的基本域。我们可以证明,$L$ 的所有基本域,体积都是一样的。于是我们给出下面的重要定义:
行列式(determinant) 设 $L$ 是一个 $n$ 维 lattice,$\F$ 是其基本域。那么 $\F$ 的 $n$ 维度量(面积,体积,etc.)称为 $L$ 的行列式(determinant,翻译成行列式显然是不恰当的,但由于英文里面的行列式也是 determinant,这个地方没法翻译成别的东西),或称 $L$ 的协体积(covolume,这个地方也是不太恰当的,因为 $L$ 本身显然并没有协体积。实际上这是 $\R ^n$ 商掉 $L$ 得到的集合,即一个基本域的协体积)。记为 $\det(L)$.
接下来,我们研究一下 lattice 的协体积。如果我们将 lattice 的协体积视为 basis $\vn$ 所围成的平行体 $\F$ 的协体积,若这些基向量长度固定的话,想要得到最大的协体积,必然各个向量之间都要正交(类比于,相同长度的四条线段围成平行四边形,当其恰好为正方形的时候面积最大)。于是我们得到了 lattice 协体积的上限:
(Hadamard 不等式) 设 $L$ 是一个 lattice,取其任意一个基 $\vn$,设 $\F$ 是 $L$ 的一个基本域。那么有 $$\det L = \text{Vol}(\F)\leq \|\v_1\| \|\v_2\| \cdots \|\v_n\|$$
其中,basis 的各个向量越像正交的,则协体积越接近上限。当 basis 各个向量恰好正交时,上面的 Hadamard 不等式取到等号。
至于如何求行列式,我们下面给出 $L \subset \R ^n$ 的维度恰等于 $n$ 时的计算方法。
设 $L\subset \R ^n$ 是一个 $n$ 维 lattice,设 $\vn$ 是基,$\F$ 是对应的基本域。接下来我们写出各个基向量的坐标:$$\v_i = (r _{i1}, r _{i2}\do r _{in})$$
把这些坐标写进矩阵里面:$$F = F(\vn) = \begin{pmatrix} r _{11} & r _{12} & \cdots & r _{1n} \\ r _{21} & r _{22} & \cdots & r _{2n} \\ \vdots & \vdots & \ddots & \vdots \\ r _{n1} & r _{n2} & \cdots & r _{nn} \end{pmatrix}$$
则可以如下计算 $\F$ 的协体积:$$\text{Vol}\left( \F(\vn) \right) = \left| \det F \right|$$
证明需要利用到微积分,我们略掉。总之,如果 lattice 的维度与空间的维度恰好相等,则我们只需要计算基向量的系数矩阵的行列式,即可得到 lattice 的协体积。举个例子:之前代码里面的 lattice $L$,其协体积为 $$\det L = |\det A| = \left| \det \begin{pmatrix} 2 & 1 & 3 \\ 1 & 2 & 0 \\ 2 & -3 & -5 \end{pmatrix} \right| = |-36| = 36$$
容易验证,从另一个基计算出来的协体积,也是相同的结果。
print(A)
# [ 2 1 3]
# [ 1 2 0]
# [ 2 -3 -5]
print(A.det())
# -36
print(B)
# [ 4 -2 -2]
# [ 5 -7 -7]
# [ 4 5 3]
print(B.det())
# 36从刚刚讲的定理,我们也可以看出来,协体积是 lattice 的固有属性,与具体用于计算的基本域无关。证明思路如下:我们先利用基 $\v_i$ 计算出协体积,然后换另一个基 $w_j$ 用于计算。由于 $W = U \cdot V$,其中 $U$ 为基变换矩阵,其行列式为 $\pm 1$,于是 $\det W = \det U \det V$,显然其绝对值仍然等于 $\det V$ 的绝对值。证毕。
